Construction of a Haar measure on the projective limit group and random order values of non-atomic games

Abstract

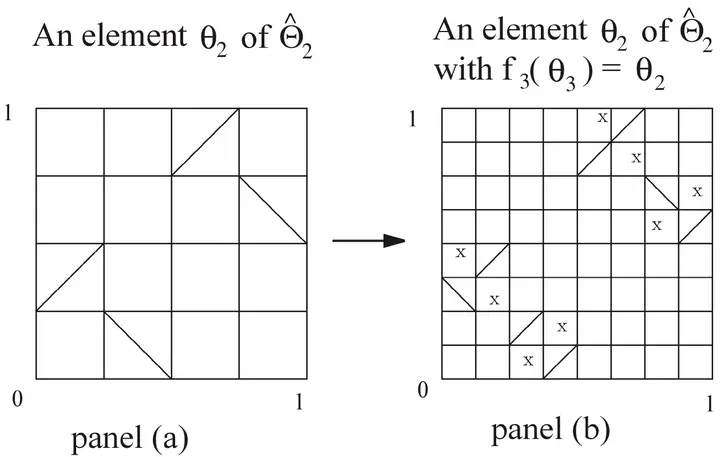
This paper constructs an increasing sequence of finite measurable subgroups of Lebesgue measure preserving (l.m.p.) automorphisms of the unit interval, and projective Borel homomorphisms of the subgroups. Then, by superimposing this group structure on the original Daniel-Kolmogorov model of stochastic processes it extends the DanielKolmogorov consistency theorem which enables the construction of a separated measurable projective limit group and its representation as an uncountably large subgroup of l.m.p. automorphisms. Each such automorphism induces a distinct ordering of the players in the unit interval. With respect to this group of random orders, and again using the extended consistency theorem, a formula for the unique random order value operator, proposed by Raut, (Indian Statistical Institute discussion paper no. 8108, 1981) and Raut (Random order approach to Shapley-value of games and Haar measure (mimeo), 1993, University of California-San Diego), is derived for economically important classes of scalar and vector measure valued games in pNA. The formula is seen to be identical to the axiomatic value formula of Aumann and Shapley (values of non-atomic games, 1974, Princeton University Press).